Civil Engineering:
Principles of Statics; Geometrical Properties of Areas
If a body remains in equilibrium under a system of force, the following conditions obtain:
1. The algebraic sum of the components of the force in any given directions is zero.
2. the algebraic sum of the moments of the forces with respect to any given axis is zero.
Equations of Equilibrium:
The above statements are verbal expressions of the equations of equilibrium. In
the absence of any notes to the contrary, a clockwise moment is considered positive; a counter clockwise moment, negative.
The body in Fig. 1a is acted on by forces A, B, and C, as shown. Draw the vector representing the equilibrant of the system.
Calculation Procedure:
1. Construct the system force line
In Fig.1b, draw the vector chain A-B-C, which is termed the force line. The vector
extending from the initial point to the terminal point of the force line represents the
resultant R. In any force system, the resultant R is equal to and collinear with the
equilibrium E but acts in the opposite direction. The equilibrium of a force system is
a single force that will balance the system.
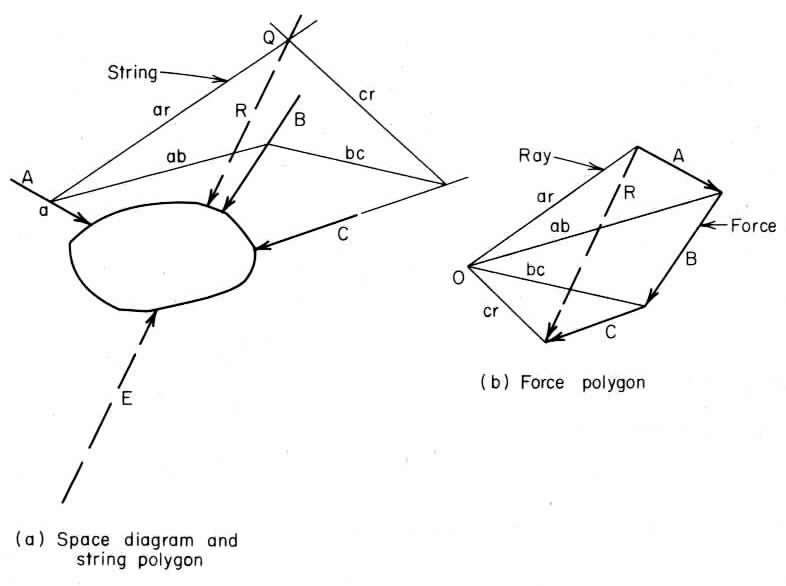
Fig. 1
|
2. Construct the system rays
Selecting an arbitary point O as the pole, draw the rays from O to the ends of the
vector and label them as shown in Fig.1b.
3. Construct the string polygon
In Fig.1a, construct the string polygon as follows:
At an arbitrary point a on the action line of force A, draw strings parallel to the
rays ar and ab.
At the point where the string ab intersects the action line of force B, draw a string
parallel to ray bc.
At the point where string bc intersects the action line of force C, draw a string
parallel to cr. The intersection point Q of ar and cr lies on the action line of R.
4. Draw the vector for the resultant and equilibrant
In Fig.1a, draw the vector representing R. Establish the magnitude and direction
of this vector from the force polygon. The action line of R passes through Q.
Lastly, draw a vector equal to and collinear with that representing R but opposite
in direction. This vector represents the equilibrant E.
Related Calculations:
Use this general method for any force system acting in a single plane.
With a large number of forces, the resultant of a smaller number of forces can
be combined with the remaining forces to simplify the construction.
